Опис властивостей матеріалів в хвильових електромагнітних задачах

1. Які рівняння ми вирішуємо?
2. електропровідність
3. Відносна діелектрична проникність
4. Відносна магнітна проникність
5. Зауваження по моделюванню і побудови сіток
6. висновок

Всякий раз, коли ми вирішуємо електродинамічну задачу в середовищі COMSOL Multiphysics, ми будуємо модель, що складається з областей і граничних умов. Усередині областей, ми використовуємо різні моделі для опису та подання широкого спектру матеріалів і їх властивостей. Однак, з математичної точки зору, всі ці різні матеріали, в кінцевому підсумку підкоряються одному і тому ж основного рівняння. Давайте більш детально розглянемо ці різні моделі матеріалів і обговоримо, коли їх слід використовувати.

Які рівняння ми вирішуємо?

У даній статті, ми будемо мати на увазі частотно-залежну форму рівнянь Максвелла в інтерфейсі Electromagnetic Waves, Frequency Domain (Електромагнітні Хвилі, Частотная Область) доступному як в модулі Радіочастоти, так і в модулі Хвильова Оптика. Представлена ​​тут інформація може бути застосована в т.ч. для формулювань використовувані в інтерфейсі Electromagnetic Waves, Beam Envelopes (Електромагнітні Хвилі, огинає Пучка) в модулі Хвильова Оптика.

У припущенні лінійності відгуку матеріалу від напруженості поля, основні рівняння Максвелла для частотної області можуть бути представлені у вигляді:

\ Nabla \ times \ left (\ mu_r ^ {- 1} \ nabla \ times \ mathbf {E} \ right) - \ frac {\ omega ^ 2} {c_0 ^ 2} \ left (\ epsilon_r - \ frac {j \ sigma} {\ omega \ epsilon_0} \ right) \ mathbf {E} = 0

Рішення цього рівняння шукається для вектора напруженості електричного поля, \ mathbf {E}, з робочою частотою \ omega = 2 \ pi f (c_0 - швидкість світла у вакуумі). Інші позначення описують властивості матеріалу: \ mu_r, відносна магнітна проникність ; \ Epsilon_r, відносна діелектрична проникність ; і \ sigma, електрична провідність . Всі ці матеріальні параметри можуть бути позитивними або негативними, дійсними або комплексними числами, а також можуть бути скалярними або тензорними величинами. Властивості матеріалу можуть також змінюватися в залежності від частоти, хоча і не завжди обов'язково враховувати ці зміни, якщо рішення шукається тільки у відносно вузькому діапазоні частот.

Давайте тепер розглянемо докладніше кожне з цих матеріальних властивостей.

електропровідність

Електропровідність є кількісною мірою того, наскільки добре матеріал проводить струм - це величина обернена до питомій електричному опору. Провідність матеріалу вимірюється при стаціонарних умовах (постійному струмі) і, як можна помітити з наведеного вище рівняння, з ростом частоти, ефективне питомий опір матеріалу зростає. Зазвичай передбачається, що провідність не змінюється з частотою. Пізніше, ми також розглянемо різні моделі матеріалів з частотно-залежною провідністю.

У будь-якому матеріалі з ненульовий провідністю, в доданому електричному полі, буде виникати електричний струм і відбуватися розсіювання енергії, відоме як резистивні втрати, які також називають Джоулевоим нагріванням . Найчастіше це викликає відчутне підвищення температури, яка буде змінювати провідність. Для обліку зміни провідності з температурою, ви можете задати будь-яку функціональну залежність або використовувати експериментальні дані. Можна також скористатися вбудованою моделлю лінеаризованого питомої опору.

Linearized Resistivity (лінеаризоване модель резистивности) - це часто застосовується модель для обліку залежно провідності від температури за формулою:

\ Sigma = \ frac {1} {\ rho_0 (1 + \ alpha (T-T_ {ref}))}

де \ rho_0 - питомий опір при референсной температурі, T_ {ref} - референсна температура, і \ alpha є температурним коефіцієнтом питомої опору. Просторово-неоднорідне поле температури, T, може або задаватися, або розраховуватися в процесі вирішення.

Провідність вводиться як дійсне число, але вона може бути анізотропної величиною, що означає, що провідність матеріалів різниться в різних координатних напрямках. Такий підхід видається цілком доцільним, коли у вас є, наприклад, шаруватий матеріал, в якому ви не бажаєте явно моделювати окремі шари. Для композитного матеріалу можна ввести якусь усереднену провідність, яка буде або визначатися експериментально або обчислюватися в результаті окремого аналізу.

У модулі Радіочастоти, є ще два варіанти для обчислення усередненої провідності: закон Арчі для обчислення ефективної провідності непроводящей пористого середовища, заповненої токопроводящей рідиною і модель пористого середовища для суміші матеріалів.

Archie's Law (Закон Арчі) є моделлю, як правило, використовується для моделювання грунтів, насичених морською водою або сирою нафтою, тобто рідинами з відносно високою провідністю в порівнянні з грунтом.

Porous Media (Пориста середа) - це група моделей: є три різні варіанти розрахунку ефективної провідності для суміші, що включає аж до п'яти компонентів. По-перше, Volume Average, Conductivity (Усереднення по Обсягом для провідності), яке формулюється як:

\ Sigma_ {eff} = \ sideset {} {^ n_ {i = 1}}
\ Sum \ theta_i \ sigma_i

де \ theta є парціальний обсяг кожного матеріалу - частина обсягу, займаного кожним з матеріалів суміші. Ця модель підходить, коли провідності матеріалів мають схожі значення. Якщо ж провідності абсолютно різні, тоді формулювання Volume Average, Resistivity (Усереднення за обсягом для разістівності) є більш придатною:

\ Frac {1} {\ sigma_ {eff}} = \ sideset {} {^ n_ {i = 1}}
\ Sum \ frac {\ theta_i} {\ sigma_i}

Нарешті, формулювання Power Law (Статечної Закон) дасть значення провідності, що лежить між двох інших формулювань:

\ Sigma_ {eff} = \ sideset {} {^ n_ {i = 1}}
\ Prod \ sigma_i ^ {\ theta_i}

Всі ці моделі застосовні тільки в випадках, коли масштаб довжини, на якій матеріали значною мірою змінюють свої властивості, набагато менше, ніж довжина хвилі.

Відносна діелектрична проникність

Відносна діелектрична проникність є кількісною мірою того, наскільки добре матеріал поляризується у відповідь на прикладена електричне поле. Прийнято будь-який матеріал з \ epsilon_r> 1 називати діелектричним матеріалом , Хоча навіть вакуум (\ epsilon_r = 1) можна назвати діелектриком. Широке поширення отримав також термін діелектрична постійна для випадків, коли хочуть послатися на відносну діелектричну проникність матеріалів.

Відносна діелектрична проникність матеріалів часто задається у вигляді комплексного числа, де негативна уявна частина являє собою втрати в матеріалі при зміні вектором електричного поля свого напрямку з плином часу. Будь-який матеріал, який зазнає впливу змінюється в часі електричного поля, буде розсіювати частина електричної енергії у вигляді тепла. відомі як діелектричні втрати , Вони є наслідком зміни форми електронних хмар навколо атомів під впливом електричного поля. Діелектричні втрати концептуально відрізняються від резистивних втрат, які обговорювалися раніше; однак, з математичної точки зору, вони, насправді, описуються однаково - як комплексно-значний член в основному рівнянні. Майте на увазі, що в середовищі COMSOL Multiphysics передбачається, що негативна уявна частина (позитивне значення електропровідності) відповідає втратам, в той час як позитивна уявна частина комплексної діелектричної проникності (від'ємне значення електропровідності) пріведовіт до наростання (тобто генерації) випромінювання всередині матеріалу.

Існує сім різних моделей матеріалів для відносної діелектричної проникності. Розглянемо кожну з цих моделей.

Relative Permittivity (Відносна діелектрична проникність) є опцією за замовчуванням для модуля Радіочастоти. Можна вводити дійсні або комплексні, скалярні або тензорні величини. Моделі типу Porous Media, аналогічні описаним вище в розділі про електричну провідність, можуть використовуватися для відносної діелектричної проникності.

Refractive Index (Показник заломлення) є опцією за замовчуванням для модуля Хвильова Оптика. Ви окремо вводите дійсну і уявну частини показника заломлення, що позначаються n і k, і відносна діелектрична проникність при цьому представляється як \ epsilon_r = (n-jk) ^ 2. Ця модель матеріалу передбачає нульове значення провідності і рівність одиниці магнітної проникності.

Loss Tangent (Тангенс кута діелектричних втрат) вимагає завдання дійсної величини для відносної діелектричної проникності, \ epsilon_r & # 39, і скалярною величини для тангенса втрат, \ delta. Відносна діелектрична проникність обчислюється як \ epsilon_r = \ epsilon_r & # 39 (1-j \ tan \ delta), при цьому провідність матеріалу дорівнює нулю.

Опція Dielectric Loss (Діелектричні Втрати) є варіантом введення дійсної і уявної частин відносної діелектричної проникності \ epsilon_r = \ epsilon_r & # 39-j \ epsilon_r & # 39 & # 39. Будьте уважні по відношенню до знака: введення позитивного дійсного числа для уявної частини \ epsilon_r & # 39 & # 39 при використанні цього інтерфейсу призведе до втрат в моделі (див.вище), так як множення на -j виконується всередині програмного забезпечення. Прикладом використання даної моделі матеріалу, може послужити навчальна модель Оптичне розсіювання на золотий наносфер .

Drude-Lorentz Dispersion (Дисперсія Друде-Лоренца) є моделлю матеріалів, розробленої на основі моделі вільних електронів Друде і моделі осцилятора Лоренца. Модель Друде (при \ omega_0 = 0) використовується для металів і легованих напівпровідників, а модель Лоренца описує резонансні явища, такі як фононні моди і міжзонного переходи. З суммирующим членом, комбінація цих двох моделей дозволяє досить точно описувати широкий спектр твердих матеріалів. Дана модель передбачає частотну залежність комплексної відносної діелектричної проникності у вигляді:

\ Epsilon_r = \ epsilon _ {\ infty} + \ sideset {} {^ M_ {k = 1}}
\ Sum \ frac {f_k \ omega_p ^ 2} {\ omega_ {0k} ^ 2 \ omega ^ 2 + i \ Gamma_k \ omega}

де \ epsilon _ {\ infty} позначає високочастотний внесок у відносну діелектричну проникність, \ omega_p - плазмова частота, f_k - сілиосцілляторов, \ omega_ {0k} є резонансними частотами, а \ Gamma_k - коефіцієнти загасання. Оскільки дана модель обчислює комплексно-значну діелектричну проникність, провідність в середовищі COMSOL Multiphysics встановлюється рівною нулю. Цей підхід є одним із способів моделювання частотно-залежною провідності.

Debye Dispersion (Дисперсія Дебая) є моделлю матеріалу, розробленої Пітером Дебаєм, і грунтується на часи релаксації поляризації. В першу чергу модель актуальна для полярних рідин. Вона використовує такий вигляд частотної залежності комплексної відносної діелектричної проникності:

\ Epsilon_r = \ epsilon _ {\ infty} + \ sideset {} {^ M_ {k = 1}}
\ Sum \ frac {\ Delta \ epsilon_k} {1 + i \ omega \ tau_k}

де \ epsilon _ {\ infty} позначає високочастотний внесок у відносну діелектричну проникність, \ Delta \ epsilon_k внесок k-го процесу для відносної діелектричної проникності та \ tau_k є час релаксації. Оскільки дана модель обчислює комплексно-значну діелектричну проникність, провідність передбачається рівний нулю. Це ще один альтернативний спосіб для моделювання частотно-залежною провідності.

Sellmeier Dispersion (Дисперсія Зельмейера) доступна в модулі Хвильова Оптика і, як правило, використовується для оптичних матеріалів. Передбачається рівність нулю провідності і одиниці магнітної проникності, а відносна діелектрична проникність визначається через робочу довжину хвилі, \ lambda, а не частоти:

\ Epsilon_r = 1 + \ sideset {} {^ M_ {k = 1}}
\ Sum \ frac {B_k \ lambda ^ 2} {\ lambda ^ 2-C_k}

де коефіцієнти B_k і C_k визначають відносну діелектричну проникність.

Вибір між цими моделями визначається тим, які саме властивості матеріалу доступні для вас в технічній літературі / довідниках. Зверніть увагу, що на математичній мові все вони входять в основне рівняння ідентичним чином.

Відносна магнітна проникність

Відносна магнітна проникність є кількісною мірою того, яким чином матеріал реагує на прикладена магнітне поле. Будь-який матеріал з \ mu_r> 1 зазвичай називається магнітним матеріалом (або магнетиком). Найбільш поширеним магнітним матеріалом на Землі є залізо, але чисте залізо рідко застосовується в радіотехнічних або оптичних додатках. Набагато частіше мають справу з феррімагнітном матеріалами (або, феримагнетика - не плутати з феромагнетиками). Такі матеріали виявляють сильні магнітні властивості з анізотропією, яка управляється постійним зовнішнім магнітним полем. На відміну від заліза, феррімагнітниє матеріали мають низьку провідність, так що високочастотні електромагнітні поля здатні проникати вглиб і взаємодіяти з об'ємом матеріалу. Дана навчальна модель демонструє яким чином можна описувати і моделювати феррімагнітниє матеріали в СВЧ-діапазоні.

У розпорядженні є два доступних варіанти для завдання відносної магнітної проникності: модель Relative Permeability (Відносна магнітна проникність), яка використовується за умовчанням в модулі Радіочастоти і модель Magnetic Losses (Магнітні втрати). Модель Relative Permeability дозволяє вводити речові або комплексні, скалярні або тензорні величини. Моделі типу Porous Media, аналогічні описаним раніше в розділі про провідність, можуть використовуватися для відносної магнітної проникності. Модель Magnetic Losses аналогічна описаній вище моделі Dielectric Loss в тому, що дійсна і уявна частини відносної магнітної проникності вводяться як речові числа. Уявна частина проникності призводить до магнітних втрат в матеріалі.

Зауваження по моделюванню і побудови сіток

При будь-якому моделюванні електромагнітних явищ, однією з найважливіших речей, яку необхідно мати на увазі, є поняття глибини скін-шару, - відстані всередині матеріалу, на якому полі спадає в 1 / e раз від свого значення на поверхні. Глибина скін-шару визначається з виразу:

\ Delta = \ left [\ operatorname {Re} \ left (\ sqrt {j \ omega \ mu_0 \ mu_r (\ sigma + j \ omega \ epsilon_0 \ epsilon_r)} \ right) \ right] ^ {- 1}

де, як ми бачили, відносна діелектрична і магнітна проникності можуть приймати комплексні значення.

Вам необхідно завжди контролювати глибину скін-шару і порівнювати її з характерними розмірами областей в своїй моделі. Якщо глибина скін-шару виявиться набагато менше розмірів об'єкта, можна замість безпосереднього моделювання цієї області скористатися для неї граничними умовами, як описано тут: " Моделювання металевих об'єктів в хвильових електромагнітних задачах ". Якщо глибина скін-шару порівнянна або більше розмірів об'єкта, то електромагнітні поля почнуть проникати вглиб об'єкта.

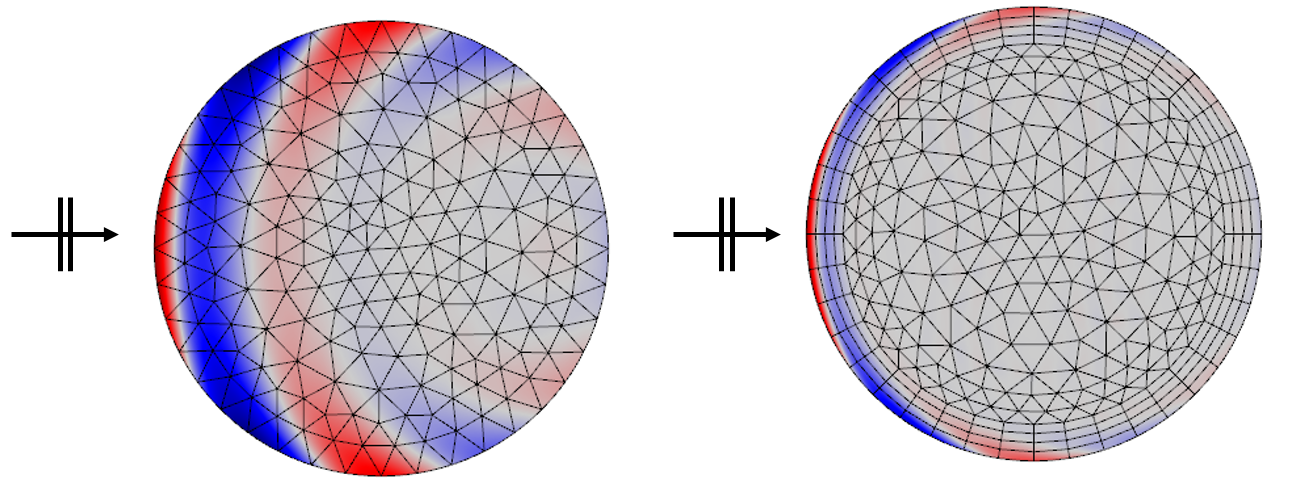
Плоска хвиля падає на об'єкти з різними проводимостями і, отже, з различающимися розмірами скін-шарів. Коли глибина скін-шару виявляється менше довжини хвилі, використовується сіткове розбиття на основі пограслойних елементів, показане праворуч. Також наведено графічне відображення розподілу електричного поля.

Якщо глибина скін-шару менше розмірів об'єкта, то рекомендується використовувати сіткове розбиття на основі пограслойних елементів для вирішення різких змін поля у напрямку нормалі до кордону, мінімум з одним елементом на скін-шар і мінімум трьома елементами в прикордонному шарі. Якщо глибина скін-шару більше ефективної довжини хвилі в середовищі, то для необхідного дозволу досить мати стандартне розбиття з п'ятьма елементами на довжину хвилі в середовищі, як показано зліва на малюнку вище.

висновок

У цій статті ми розглянули різні варіанти, наявні в середовищі COMSOL Multiphysics, для завдання властивостей матеріалу при моделюванні електродинамічних задач. Ми побачили, що математичні моделі матеріалів, в яких визначається відносна діелектрична проникність, підходять навіть для металів в певному діапазоні частот. З іншого боку, ми також можемо описувати металеві області за допомогою граничних умов, як зазначалося раніше в нашому корпоративному блозі . Поряд з більш ранніми статтями з моделювання відкритих кордонів і налаштування різних типів портів , Ми, до теперішнього часу, охопили практично всі основні аспекти електродинамічного чисельного моделювання задач. Однак, це не все, що ми хочемо вам розповісти, так що, слідкуйте за оновленнями!