Основні поняття кінематики
Кінематика - розділ механіки, який вивчає рух тіл без урахування причин, що викликали цей рух.
Основним завданням кінематики є знаходження положення тіла в будь-який момент часу, якщо відомі його положення, швидкість і прискорення в початковий момент часу.
Механічний рух - це зміна положення тіл (або частин тіла) відносно один одного в просторі з плином часу.
Для опису механічного руху треба вибрати систему відліку.
Тіло відліку - тіло (або група тіл), прийняте в даному випадку за нерухоме, щодо якого розглядається рух інших тіл.
Система відліку - це система координат, пов'язана з тілом відліку, і обраний спосіб вимірювання часу (рис. 1).
Мал. 1
Положення тіла можна визначити за допомогою радіуса-вектора \ (~ \ vec r \) або за допомогою координат.
Радіус-вектор \ (~ \ vec r \) точки Μ - спрямований відрізок прямої, що з'єднує початок відліку Про з точкою Μ (рис. 2).
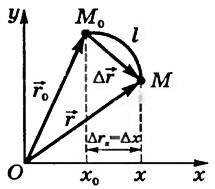
Мал. 2
Координата x точки Μ - це проекція кінця радіуса-вектора точки Μ на вісь Ох. Зазвичай користуються прямокутною системою до ординат. У цьому випадку положення точки Μ на лінії, площині і в просторі визначають відповідно одним (x), двома (х, у) і трьома (х, у, z) числами - координатами (рис. 3).
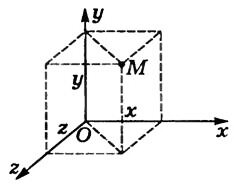
Мал. 3
В елементарному курсі фізики вивчають кинематику руху матеріальної точки.
Матеріальна точка - тіло, розмірами якого в даних умовах можна знехтувати.
Цією моделлю користуються в тих випадках, коли лінійні розміри розглянутих тел багато менше всіх інших відстаней в даній задачі або коли тіло рухається поступально.
Поступальним називається рух тіла, при якому пряма, що проходить через будь-які дві точки тіла, переміщається, залишаючись паралельною самій собі. При поступальному русі всі точки тіла описують однакові траєкторії і в будь-який момент часу мають однакові швидкості і прискорення. Тому для опису такого руху тіла достатньо описати рух його однією довільної точки.
Надалі під словом "тіло" будемо розуміти "матеріальна точка".
Лінія, яку описує рух тіло в певній системі відліку, називається траєкторією. На практиці форму траєкторії задають за допомогою математичних формул (y = f (x) - рівняння траєкторії) або зображують на малюнку. Вид траєкторії залежить від вибору системи відліку. Наприклад, траєкторією тіла, що вільно падає в вагоні, який рухається рівномірно і прямолінійно, є пряма вертикальна лінія в системі відліку, пов'язаної з вагоном, і парабола в системі відліку, пов'язаної з Землею.
Залежно від виду траєкторії розрізняють прямолінійний і криволінійний рух.
Шлях s - скалярна фізична величина, яка визначається довжиною траєкторії, описаної тілом за певний проміжок часу. Шлях завжди позитивний: s> 0.
Переміщення \ (~ \ Delta \ vec r \) тіла за певний проміжок часу - спрямований відрізок прямої, що сполучає початкове (точка M 0) і кінцеве (точка М) положення тіла (див. Рис. 2):
\ (~ \ Delta \ vec r = \ vec r - \ vec r_0, \)
де \ (~ \ vec r \) і \ (~ \ vec r_0 \) - радіуси-вектори тіла в ці моменти часу.
Проекція переміщення на вісь Ox \ [~ \ Delta r_x = \ Delta x = x - x_0 \], де x 0 і x - координати тіла в початковий і кінцевий моменти часу.
Модуль переміщення не може бути більше шляху \ [~ | \ Delta \ vec r | \ Le s \].
Знак рівності відноситься до випадку прямолінійного руху, якщо напрямок руху не змінюється.
Знаючи переміщення і початкове положення тіла, можна знайти його положення в момент часу t:
\ (~ \ Vec r = \ vec r_0 + \ Delta \ vec r; \) \ (~ \ left \ {\ begin {matrix} x = x_0 + \ Delta r_x; \\ y = y_0 + \ Delta r_y. \ end {matrix} \ right. \)
Швидкість - міра механічного стану тіла. Вона характеризує швидкість зміни положення тіла щодо даної системи відліку і є векторної фізичною величиною.
Середня швидкість \ (~ \ mathcal h \ vec \ upsilon \ mathcal i \) - векторна фізична величина, чисельно рівна відношенню переміщення до проміжку часу, за який воно відбулося, і спрямована уздовж переміщення (рис. 4):
\ (~ \ Mathcal h \ vec \ upsilon \ mathcal i = \ frac {\ Delta \ vec r} {\ Delta t}; \ qquad \ mathcal h \ vec \ upsilon \ mathcal i \ upuparrows \ Delta \ vec r. \ ) 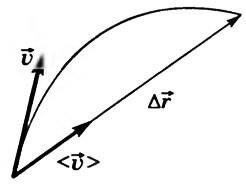 Мал. 4
Мал. 4
В СІ одиницею швидкості є метр в секунду (м / с).
Середня швидкість, знайдена за цією формулою, характеризує рух тільки на тій ділянці траєкторії, для якого вона визначена. На іншій ділянці траєкторії вона може бути іншою.
Іноді користуються середньою швидкістю шляху \ [~ \ mathcal h \ upsilon \ mathcal i = \ frac {s} {\ Delta t} \], де s - шлях, пройдений за проміжок часу Δ t. Середня швидкість шляху - це скалярна величина.
Миттєва швидкість \ (~ \ vec \ upsilon \) тіла - швидкість тіла в даний момент часу (або в даній точці траєкторії). Вона дорівнює межі, до якої прагне середня швидкість за нескінченно малий проміжок часу \ (~ \ vec \ upsilon = \ lim _ {\ Delta t \ to 0} \ frac {\ Delta \ vec r} {\ Delta t} = \ vec r \ '\). Тут \ (~ \ vec r \ '\) - похідна від радіуса-вектора за часом.
У проекції на вісь Ох:
\ (~ \ Upsilon_x = \ lim _ {\ Delta t \ to 0} \ frac {\ Delta x} {\ Delta t} = x '. \)
Миттєва швидкість тіла спрямована по дотичній до траєкторії в кожній її точці в бік руху (див. Рис. 4).
Прискорення - векторна фізична величина, що характеризує швидкість зміни швидкості. Воно показує, на яку величину змінюється швидкість тіла за одиницю часу.
Середнє прискорення - фізична величина, що чисельно дорівнює відношенню зміни швидкості до часу, протягом якого воно сталося:
\ (~ \ Mathcal h \ vec a \ mathcal i = \ frac {\ Delta \ vec \ upsilon} {\ Delta t} = \ frac {\ vec \ upsilon - \ vec \ upsilon_0} {\ Delta t}. \)
Вектор \ (~ \ mathcal h \ vec a \ mathcal i \) спрямований паралельно вектору зміни швидкості \ (~ \ Delta \ vec \ upsilon \) (\ (~ \ mathcal h \ vec a \ mathcal i \ upuparrows \ Delta \ vec \ upsilon \)) в сторону угнутості траєкторії (рис. 5).
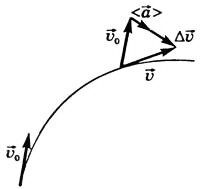
Мал. 5
Миттєве прискорення:
\ (~ \ Vec a = \ lim _ {\ Delta t \ to 0} \ frac {\ Delta \ vec \ upsilon} {\ Delta t} = \ vec \ upsilon \ '. \)
В СІ одиницею прискорення є метр на секунду в квадраті (м / с2).
У загальному випадку миттєве прискорення направлено під кутом до швидкості. Знаючи траєкторію, можна визначити напрям швидкості, але не прискорення. Напрямок прискорення визначається напрямом рівнодіюча сил, що діють на тіло.
При прямолінійному русі зі зростаючою за модулем швидкістю (рис. 6, а) вектори \ (~ \ vec a \) і \ (~ \ vec \ upsilon_0 \) сонаправлени (\ (~ \ vec a \ upuparrows \ vec \ upsilon_0 \) ) і проекція прискорення на напрямок руху позитивна.
При прямолінійному русі з порядку спадання В порядку модулю швидкістю (рис. 6, б) напрями векторів \ (~ \ vec a \) і \ (~ \ vec \ upsilon_0 \) протилежні (\ (~ \ vec a \ uparrow \ downarrow \ vec \ upsilon_0 \)) і проекція прискорення на напрямок руху негативна.
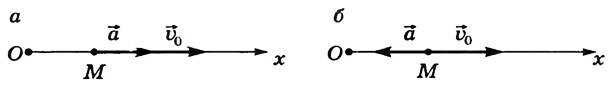
Мал. 6
Вектор \ (~ \ vec a \) при криволінійному русі можна розкласти на дві складові, спрямовані уздовж швидкості \ (~ \ vec a _ {\ tau} \) і перпендикулярно швидкості \ (~ \ vec a_n \) (рис. 1.7), \ (~ \ vec a _ {\ tau} \) - тангенціальне прискорення, що характеризує швидкість зміни модуля швидкості при криволінійному русі, \ (~ \ vec a_n \) - нормальне прискорення, що характеризує швидкість зміни напрямку вектора швидкості при криволінійному русі Модуль прискорення \ ( ~ a = \ sqrt {a ^ 2 _ {\ tau} + a ^ 2_n} \).
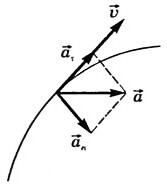
Мал. 7
література
- Аксеновіч Л.А. Фізика в середній школі: Теорія. Завдання. Тести: Учеб. посібник для установ, що забезпечують отримання заг. середовищ, освіти / Л.А. Аксеновіч, Н.Н.Ракіна, К.С. Фаріно; Під ред. К.С. Фаріно. - Мн .: Адукация i вихаванне, 2004. - C.5-8.
