- Лінійна алгебра: від Гаусса до суперкомп'ютерів майбутнього В.П.Ільін,доктор фізико-математичних наук,професор,...
- Введення: історія, передумови та проблеми
- Зовсім алгебраїчна, але дуже плідна ідея
Лінійна алгебра: від Гаусса до суперкомп'ютерів майбутнього В.П.Ільін,доктор фізико-математичних наук,професор,
головний науковий співробітник Інституту обчислювальної математики і математичної геофізкі СО РАН.
Опубліковано в журналі "Природа" , N 6, 1999 г. зміст
про автора
Валерій Павлович Ільїн , Доктор фізико-математичних наук, професор, головний науковий співробітник Інституту обчислювальної математики і математичної геофізкі СО РАН. Область наукових інтересів - обчислювальна математика , інформатика , математичне моделювання . Автор понад 250 наукових статей і дев'яти монографій (частина з них написана в співавторстві).
... Повірив
Я алгеброю гармонію
А. С. Пушкін
Введення: історія, передумови та проблеми
Опубліковано в журналі "Природа" , N 6, 1999 г. зміст
Я алгеброю гармонію
А. С. Пушкін
Аж до початку XX в. алгебра залишалася "наукою про рішення рівнянь", після чого відбулося її поділ на вищу алгебру (операції з абстрактними об'єктами різної природи) і лінійну , Основа якої - матричне числення .
Нехай заради простоти 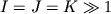 . Тоді для реалізації методу виключення Гауса потрібно виконати приблизно
. Тоді для реалізації методу виключення Гауса потрібно виконати приблизно 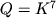 арифметичних операцій і запам'ятати
арифметичних операцій і запам'ятати 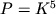 проміжних чисел. На сьогодні завдання середньої складності відповідає K = 100, що призводить до значень
проміжних чисел. На сьогодні завдання середньої складності відповідає K = 100, що призводить до значень 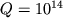 і
і 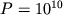 . На повсякденній мові це означає близько трьох годин роботи комп'ютера швидкодією 10 гігафлоп, тобто
. На повсякденній мові це означає близько трьох годин роботи комп'ютера швидкодією 10 гігафлоп, тобто 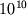 "флоп" - арифметичних операцій над "нормальними" речовими числами в секунду, при наявності оперативної пам'яті близько 10 гігабайт. Це набагато перевершує ресурси персональних комп'ютерів і робочих станцій, але на світовому ринку така ЕОМ - середнього класу. Однак якщо перейти до "великої" завданню з K = 1000, то вона вже виявляється міцним горішком навіть для рекордного суперкомп'ютера зі швидкістю в один терафлоп (
"флоп" - арифметичних операцій над "нормальними" речовими числами в секунду, при наявності оперативної пам'яті близько 10 гігабайт. Це набагато перевершує ресурси персональних комп'ютерів і робочих станцій, але на світовому ринку така ЕОМ - середнього класу. Однак якщо перейти до "великої" завданню з K = 1000, то вона вже виявляється міцним горішком навіть для рекордного суперкомп'ютера зі швидкістю в один терафлоп ( 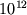 ) І пам'яттю в один терабайт.
) І пам'яттю в один терабайт.
Зовсім алгебраїчна, але дуже плідна ідея
Ідея методу неповної факторизації для вирішення алгебри
полягає в побудові такої матриці B, званої предобусловлівающей, яка легко б зверталася і була б близькою до вихідної матриці A в тому сенсі, що власні числа матриці-твори B-1A не сильно різняться між собою. Тоді послідовні наближення un будуються за допомогою ітераційного процесу , Який в канонічній записи має наступний вигляд: Тут 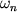 - обчислювані параметри, а число ітерацій
- обчислювані параметри, а число ітерацій 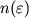 для досягнення необхідної точності
для досягнення необхідної точності 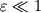 залежить від ставлення
залежить від ставлення 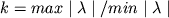 ,
,
званого числом обумовленості матриці B-1A. Ця величина k виявляється магічним числом в лінійної алгебри, характеризуючи головні обчислювальні якості будь-якої матриці, в тому числі чутливість до погрішностей заокруглень .
назад | вперед
написати коментар
Або, іншими словами, досягти заданої точності за мінімальне число арифметичних дій?

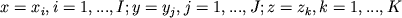 Якщо ми вирішуємо одне диференціальне рівняння другого порядку еліптичного типу (наприклад, рівняння стаціонарної дифузії або теплопровідності ), То в результаті його найпростішої апроксимації для кожного вузла (i, j, k) виходить рівняння виду
Якщо ми вирішуємо одне диференціальне рівняння другого порядку еліптичного типу (наприклад, рівняння стаціонарної дифузії або теплопровідності ), То в результаті його найпростішої апроксимації для кожного вузла (i, j, k) виходить рівняння виду 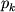 виражаються через кроки сітки і параметри вихідної задачі. Такий системі рівнянь відповідає квадратна матриця А порядку IJK з числом ненульових елементів на кожному рядку не більше 7.
виражаються через кроки сітки і параметри вихідної задачі. Такий системі рівнянь відповідає квадратна матриця А порядку IJK з числом ненульових елементів на кожному рядку не більше 7. 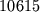 операцій в секунду до 2015 г.) - створення багатопроцесорних обчислювальних систем (до
операцій в секунду до 2015 г.) - створення багатопроцесорних обчислювальних систем (до 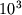 або
або 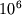 процесорів). Звідси однією з перших за актуальності проблем в обчислювальної алгебри стає розпаралелювання алгоритмів і їх відображення на архітектуру багатопроцесорних ЕОМ. Нагальність цього питання, в тому числі при вирішенні СЛАР, виникає з того загальновідомого факту, що ефективність завантаження всіх пристроїв - це хворе місце різних суперкомп'ютерів, і реалізація алгоритмів без урахування, наприклад, комунікаційних втрат може знизити фактичну продуктивність багатопроцесорної системи до декількох відсотків від її паспортних даних. Один з найефективніших методів вирішення СЛАР високого порядку базується на ітераційних алгоритмах неповної факторизації, які отримали зараз саме широке поширення в світовій обчислювальної практиці 1 . Дана стаття являє останні результати автора, що стосуються нових, перспективних підходів: узагальненого принципу компенсації в наближеною матричної факторизації , Адаптивних ітераційних методів з оптимальними впорядкованість і, нарешті, проблеми розпаралелювання алгоритмів на основі декомпозиції областей.
процесорів). Звідси однією з перших за актуальності проблем в обчислювальної алгебри стає розпаралелювання алгоритмів і їх відображення на архітектуру багатопроцесорних ЕОМ. Нагальність цього питання, в тому числі при вирішенні СЛАР, виникає з того загальновідомого факту, що ефективність завантаження всіх пристроїв - це хворе місце різних суперкомп'ютерів, і реалізація алгоритмів без урахування, наприклад, комунікаційних втрат може знизити фактичну продуктивність багатопроцесорної системи до декількох відсотків від її паспортних даних. Один з найефективніших методів вирішення СЛАР високого порядку базується на ітераційних алгоритмах неповної факторизації, які отримали зараз саме широке поширення в світовій обчислювальної практиці 1 . Дана стаття являє останні результати автора, що стосуються нових, перспективних підходів: узагальненого принципу компенсації в наближеною матричної факторизації , Адаптивних ітераційних методів з оптимальними впорядкованість і, нарешті, проблеми розпаралелювання алгоритмів на основі декомпозиції областей. 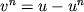 ,
, 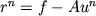
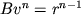 ,
, 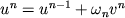 ,
, 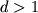 від оберненої матриці - позначимо її через
від оберненої матриці - позначимо її через 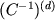 , - то знаходимо в певному сенсі наближення до зворотного матриці
, - то знаходимо в певному сенсі наближення до зворотного матриці 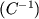 (Яка в загальному випадку щільна, тобто не містить нулів). Дійсно, якщо d збільшується аж до порядку матриці N, то
(Яка в загальному випадку щільна, тобто не містить нулів). Дійсно, якщо d збільшується аж до порядку матриці N, то 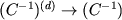 При d = N матрична апроксимація стає точної і метод вирішення СЛАР з ітераційного перетворюється в прямий, що дає точне рішення за кінцеве число дій. Фактично в цьому випадку метод наближеної факторизації переходить в блоковий метод Гаусса, який для сіткових систем рівнянь занадто дорогий.
При d = N матрична апроксимація стає точної і метод вирішення СЛАР з ітераційного перетворюється в прямий, що дає точне рішення за кінцеве число дій. Фактично в цьому випадку метод наближеної факторизації переходить в блоковий метод Гаусса, який для сіткових систем рівнянь занадто дорогий. 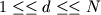 стрічкової апроксимації оберненої матриці
стрічкової апроксимації оберненої матриці